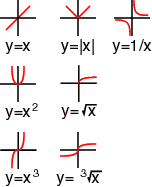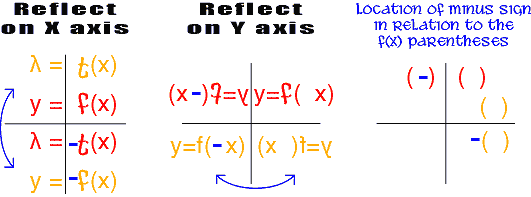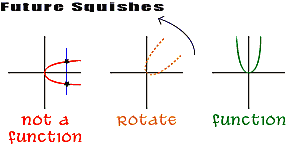Squishy Function Graphs
by T. Ford - Email me if you find any errors.
Simply:
Step 1:
Pick Function Graph |
Step 2:
Choose an Action |
Generic
Formula Adjustment |
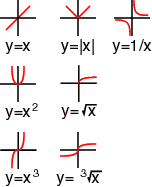 |
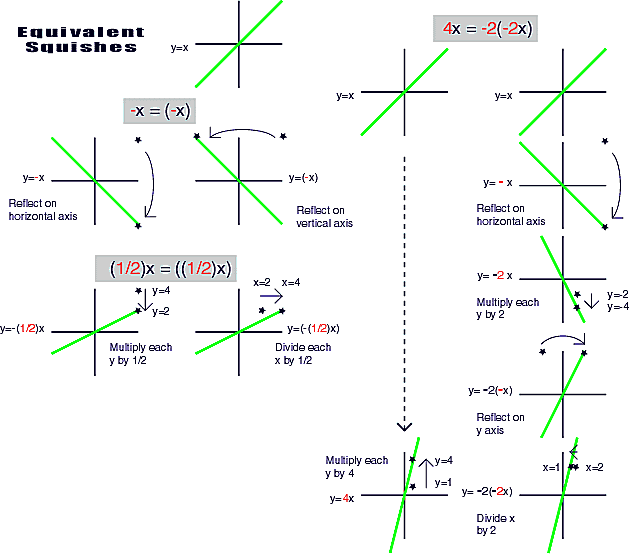
Reflect on X axis
Reflect on Y axis
Shift left
Shift right
Shift up
Shift down
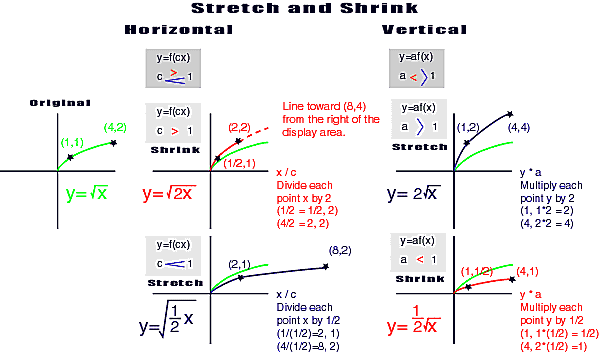
Shrink vertically
Stretch vertically
Shrink horizontally
Stretch horizontally |
y=-f(x)
y=f(-x)
y=f(x+b)
y=f(x-b)
y=f(x)+b
y=f(x)-b
y=af(x), 0<a<1
y=af(x), a>1
y=f(cx), c>1
y=f(cx), 0<c<1
|
| Step 3: Squish. See below. |
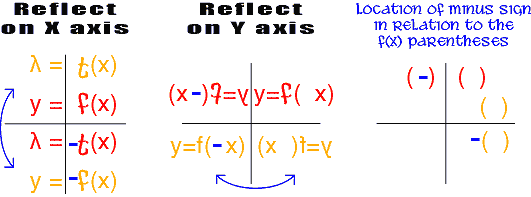
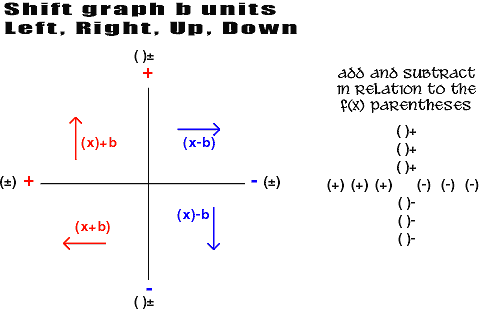

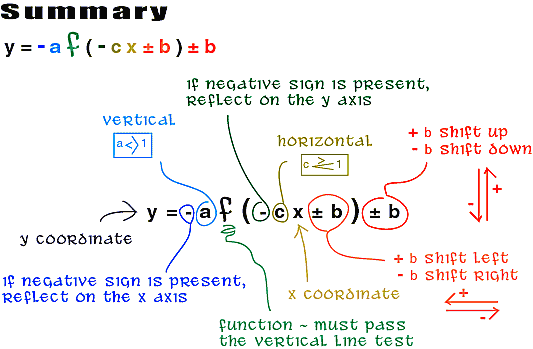
Using the above, variations on functions can be split apart.
Example 1:
y = -a|-cx + b| + d
Graph: y = |x|
Reflect on x axis. (first - sign) (make it upside down!)
If a>1, stretch vertically.
If a<1, shrink vertically.
Reflect on the y axis. (second - sign) (note: no change for absolute value graph)
If c>1, shrink horizontally.
If c<1, stretch horizontally.
Shift it left b. (for the + b inside the absolute value function)
Shift it up d. (for the + d outside the absolute value function)
Example 2:
y = -a(1/(cx - b)) + d
Graph: y = 1/x
Reflect on x axis. (first - sign) (make it upside down!)
If a>1, stretch vertically.
If a<1, shrink vertically.
Do not reflect on the y axis. (missing - sign on c)
If c>1, shrink horizontally.
If c<1, stretch horizontally.
Shift it right b. (for the - b inside the absolute value function)
Shift it up d. (for the + d outside the absolute value function)
Example 3:
y = -(1/2)x - 1
Graph y=x
Reflect on x axis. (first - sign) (make it upside down!)
Shrink vertically. ((1/2)<1)
No modifications to x, so no y axis reflection, horizontal stretching,
or horizontal shifting.
A modification to x might look like: y = -(1/2)(2x+3) - 1
Shift it down 1. (for the - 1 outside the linear function)
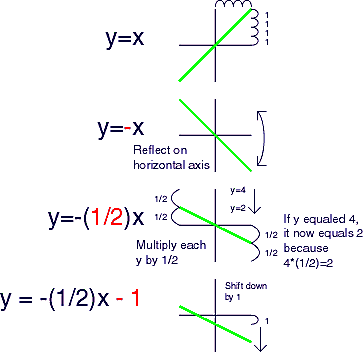
Some squishy notes: